Cet article a été rédigé dans le cadre d’un petit projet à l’Université de Versailles Saint-Quentin-en-Yvelines (UVSQ), consacré à l’étude des vibrations d’un bâtiment et des tuned mass dampers.
Version PDF disponible iciIntroduction
L’étude des vibrations des structures représente un enjeu majeur en mécanique, en particulier dans les domaines du génie civil et de la conception architecturale. Lorsqu’une structure est soumise à des sollicitations dynamiques (telles que le vent ou les séismes), elle entre en vibration. Comprendre ces phénomènes est essentiel pour garantir la stabilité, la sécurité et la durabilité des ouvrages.
L’objectif de ce travail est d’analyser le comportement vibratoire d’un bâtiment simple soumis à différentes excitations dynamiques. Pour cela, plusieurs étapes seront abordées : dans un premier temps, les principales problématiques liées aux vibrations des structures seront présentées. Un modèle physique simplifié de bâtiment, représenté par un système à un degré de liberté soumis à des oscillations forcées, sera ensuite étudié à l’aide de différentes méthodes numériques. Une attention particulière sera portée à la comparaison des résultats obtenus, ainsi qu’aux limites de chaque méthode utilisée.
Enfin, les résultats obtenus serviront à étudier les TMD (Tuned Mass Dampers, ou amortisseurs harmoniques), en s’appuyant sur l’exemple concret de la Tour Taipei 101. Cette dernière étude illustrera l’intérêt pratique de tels dispositifs d’amortissement dans le contrôle des vibrations des structures de grande hauteur.
La Tour Taipei 101
Histoire et présentation du contexte d'étude
L’étude de la dynamique des structures, et plus spécifiquement la compréhension des vibrations des bâtiments, constitue un pilier fondamental du génie civil. Elle est née de la nécessité de concevoir des ouvrages capables de résister aux sollicitations dynamiques telles que les séismes, le vent ou les charges mobiles. Ce domaine a évolué au fil des siècles, en réponse à des besoins pratiques mais aussi à des événements tragiques ayant marqué l’histoire de l’ingénierie.
Dans l’Antiquité, les bâtisseurs ne disposaient pas de modèles théoriques, mais s’appuyaient sur une intuition empirique. Les Grecs, Romains ou Égyptiens utilisaient des techniques simples pour garantir une certaine flexibilité dans les structures, par exemple en empilant des blocs ou des colonnes capables de dissiper les vibrations. Il faudra attendre les travaux de Galilée, Newton, puis ceux d’Euler et Lagrange aux XVIIe et XVIIIe siècles pour voir émerger les premières bases scientifiques de la mécanique vibratoire (1) . Ces travaux ont posé les fondements des équations du mouvement, appliquées d’abord à des systèmes simples comme les poutres et les pendules.
C’est au XXe siècle que la dynamique des bâtiments a véritablement pris son essor, notamment après les séismes majeurs de San Francisco (1906) et du Japon (1923). Ces catastrophes ont révélé les limites des conceptions purement statiques. En 1924, John R. Freeman a proposé une première modélisation de l’effet des séismes sur les structures, amorçant un tournant vers une ingénierie dynamique (2). L’apparition des accélérographes dans les années 1930 a permis de mesurer les mouvements réels du sol, donnant naissance à une approche expérimentale et à la création des premières “shake tables” pour tester les maquettes de bâtiments (1).
L’arrivée des ordinateurs dans les années 1960-1980 a marqué une révolution dans la discipline. Les ingénieurs ont pu simuler numériquement la réponse vibratoire de structures complexes, intégrer des notions avancées comme les modes propres, les fréquences naturelles ou le spectre de réponse. Le séisme de Mexico en 1985 a illustré de manière spectaculaire le phénomène de résonance sol-structure, incitant à prendre en compte les effets dynamiques dans toutes les phases de conception.
La dynamique des structures est aujourd’hui une discipline interdisciplinaire à la croisée de la mécanique, de la géotechnique, des matériaux, du traitement du signal et de l’environnement. Elle permet non seulement de garantir la sécurité des ouvrages, mais aussi d’optimiser leur confort vibratoire et leur durabilité.
Étude théorique de la réponse d’un système à un degré de liberté
Cette partie a pour objectif de présenter les bases théoriques nécessaires à l’analyse de la réponse d’un système à un degré de liberté soumis à une excitation extérieure.
Parmi l’ensemble des sollicitations possibles, nous nous intéresserons plus particulièrement à deux cas représentatifs : les excitations harmoniques, qui permettent notamment de modéliser l’action régulière du vent sur la façade d’un gratte-ciel, et les excitations de type impulsion ou réponse indicielle, utilisées pour représenter des phénomènes soudains comme les séismes.
Étude des systèmes oscillants à un degré de liberté
L’étude des systèmes oscillants à un degré de liberté (1 DDL) constitue un fondement de la mécanique vibratoire. Un tel système est généralement modélisé par une masse \(m\) soumise à une force de rappel linéaire (ressort de raideur \(k\)) et, éventuellement, à une force d’amortissement visqueux proportionnelle à la vitesse (coefficient d’amortissement \(c\) avec \(\zeta = \frac{c}{2 \sqrt{km}}\) et \(\zeta\) le rapport d'amortissement). Le mouvement du système est alors gouverné par une équation différentielle du second ordre de la forme :
$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = f(t) $$
où \(x(t)\) désigne le déplacement de la masse au cours du temps, et \(f(t)\) la force extérieure appliquée. Cette équation est linéaire et à coefficients constants, ce qui permet d’utiliser des méthodes analytiques classiques pour la résolution (3).
Méthode de résolution générale
La solution générale d’une telle équation se compose de deux parties. La première, appelée solution homogène, correspond à la solution de l’équation sans excitation externe (\(f(t) = 0\)) et décrit le comportement libre du système. Elle dépend uniquement des conditions initiales. La seconde, appelée solution particulière, correspond à la réponse forcée du système due à l’excitation externe \(f(t)\). La solution complète s’écrit donc :
$$ x(t) = x_h(t) + x_p(t) $$
où \(x_h(t)\) est la solution de l’équation homogène, et \(x_p(t)\) une solution particulière de l’équation complète (3).
Réponse à une excitation harmonique
L’un des cas les plus importants en vibration est celui d’une excitation harmonique, c’est-à-dire une force de la forme :
$$ f(t) = F_0 \cos(\omega t) $$
où \(F_0\) est l’amplitude de l’excitation, et \(\omega\) sa pulsation. Ce type d’excitation permet notamment de modéliser des forces périodiques régulières, comme celles induites par le vent ou une machine en fonctionnement, ce qui est pertinent dans le cadre de notre projet.
Pour résoudre l’équation dans ce cas, on peut utiliser la méthode des nombres complexes, en considérant une excitation de la forme complexe :
$$ f(t) = \Re\left\{ F_0 e^{i \omega t} \right\} $$
On cherche alors une solution particulière de la forme :
$$ x_p(t) = \Re\left\{ X(\omega) e^{i \omega t} \right\} $$
où \(X(\omega)\) est une constante complexe que l’on détermine en substituant dans l’équation différentielle. En remplaçant et en simplifiant, on trouve :
$$ X(\omega) = \frac{F_0}{k - m \omega^2 + i c \omega} $$
La solution particulière réelle est alors donnée par :
$$ x_p(t) = |X(\omega)| \cos(\omega t - \phi) $$
avec :
$$ |X(\omega)| = \frac{F_0}{\sqrt{(k - m \omega^2)^2 + (c \omega)^2}}, \quad \phi = \tan^{-1}\left(\frac{c \omega}{k - m \omega^2}\right) $$
Cette solution met en évidence deux phénomènes essentiels : l’amplitude de la réponse dépend fortement de la fréquence d’excitation \(\omega\), et un déphasage apparaît entre la force appliquée et la réponse du système.
Résonance et rôle de l’amortissement
Un phénomène crucial dans l’étude des systèmes vibrants est celui de la résonance. Il se produit lorsque la fréquence d’excitation \(\omega\) est proche de la fréquence propre (ou naturelle) du système non amorti, donnée par :
$$ \omega_0 = \sqrt{\frac{k}{m}} $$
En l’absence d’amortissement (\(c = 0\)), la formule précédente devient :
$$ |X(\omega)| = \frac{F_0}{|k - m \omega^2|} $$
et on observe une divergence de l’amplitude lorsque \(\omega \to \omega_0\), c’est-à-dire que le système entre en résonance, ce qui peut provoquer des vibrations de très grande amplitude, potentiellement destructrices (4).
Lorsque l’amortissement est présent (\(c > 0\)), le pic de résonance est atténué : l’amplitude maximale reste finie et se produit à une fréquence légèrement inférieure à \(\omega_0\). On peut montrer que la fréquence de résonance amortie est :
$$ \omega_r = \omega_0 \sqrt{1 - 2\zeta^2} $$
où \(\zeta = \frac{c}{2 \sqrt{km}}\) est le rapport d’amortissement. Ainsi, plus l’amortissement est important, plus le pic de résonance est atténué et déplacé vers les basses fréquences. Cela justifie l’utilisation de dispositifs d’amortissement dans les structures soumises à des sollicitations dynamiques fréquentes (4).
Un code python que nous avons réalisé (disponible en annexe) permet d'observer l'influence de l'amortissement sur le phénomène de résonance. On constate alors que la largeur du pic de résonance est d'autant plus faible (et le pic d'autant plus haut - donc plus fin) que l'amortissement est faible.
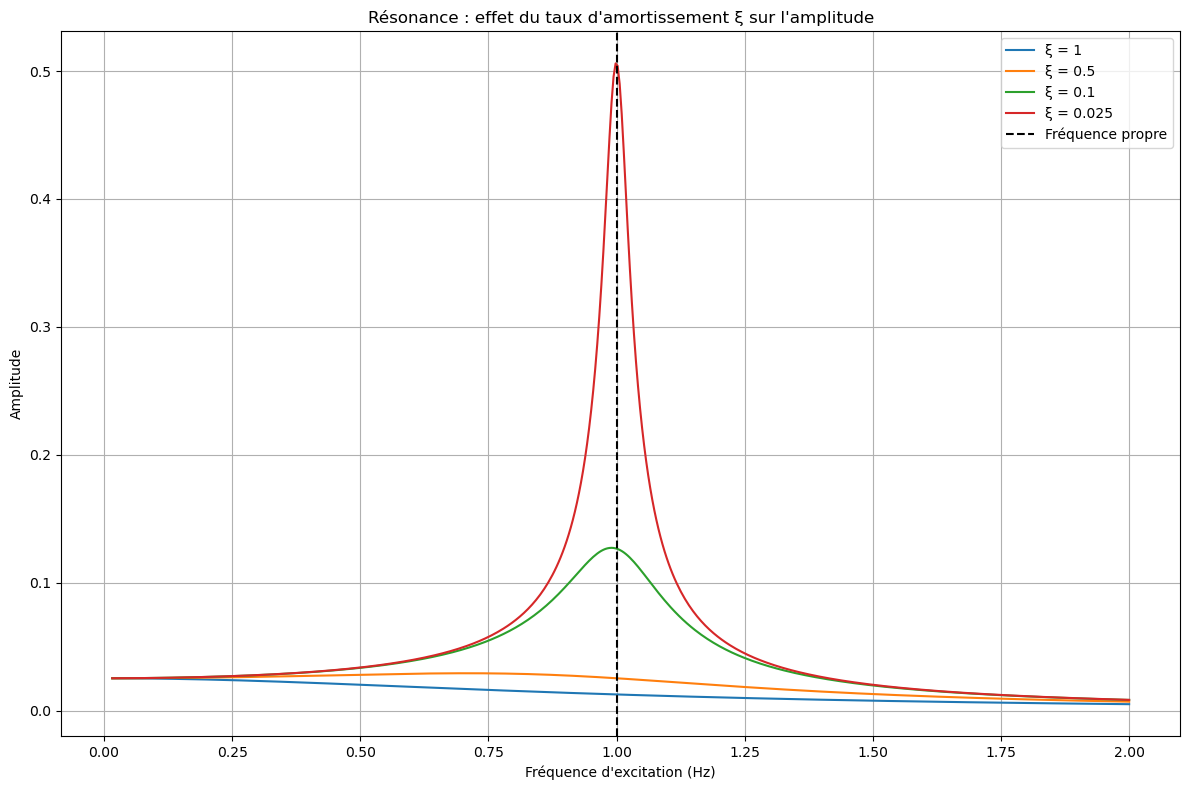Influence de \(\xi\) sur le phénomène de résonance (finesse du pic et fréquence de résonance)
Cas d'un excitation quelconque
Bien que l’excitation harmonique soit un cas fondamental, dans la réalité les sollicitations appliquées aux structures sont souvent non sinusoïdales, voire de forme complexe, comme dans le cas des séismes. Pour traiter une excitation arbitraire \(f(t)\), il est possible de décomposer ce signal en une somme de fonctions harmoniques à l’aide d’une série de Fourier. Si \(f(t)\) est périodique, on peut écrire :
$$ f(t) = \sum_{n=1}^{\infty} \left[ a_n \cos(n \omega t) + b_n \sin(n \omega t) \right] $$
Chacune de ces composantes peut être étudiée séparément, car le système est linéaire : la réponse totale du système est alors la somme des réponses individuelles à chaque composante harmonique. Cette approche permet ainsi d’étendre les résultats obtenus pour une excitation sinusoïdale à toute excitation périodique (4).
Pour des signaux transitoires quelconques, la notion de période n’a plus de sens. Il existe alors plusieurs techniques pour lever cette difficulté: l'utilisation de la transformée de Laplace ou de Fourier, la décomposition en impulsions élémentaires ou échelons élémentaires et enfin la résolution numérique directe (avec la méthode d’Euler par exemple). Nous nous intéresserons dans la suite de ce rapport à ces deux dernières méthodes.
Mise en place de méthodes numériques
Les éléments théoriques développés précédemment vont désormais servir de base à la mise en œuvre de méthodes numériques visant à étudier la réponse d’un système à un degré de liberté soumis à une excitation quelconque. Les implémentations seront réalisées en MATLAB. Cette section portera une attention particulière à l’influence des différents paramètres sur la performance et la précision de ces méthodes. Nous procéderons ensuite à une comparaison entre les différentes approches numériques, en soulignant leurs avantages et inconvénients respectifs. Enfin, nous évoquerons les principales difficultés rencontrées lors de l’implémentation. Tous les codes de cette partie sont disponibles en annexe.
Sauf mention contraire, les différents codes seront testés pour la fonction \(f(t) = 1.5 * sin(2 \pi t)\) (choisie pour modéliser l'effet du vent sur un gratte-ciel).
Décomposition impulsionnelle
Principe théorique
L’idée derrière la décomposition impulsionnelle est que toute force extérieure peut être vue comme une combinaison d’impulsions infinitésimales appliquées au fil du temps. Chacune de ces impulsions déclenche une mini-vibration indépendante, et la réponse globale du système est la superposition de toutes ces contributions. Cette méthode nous sera particulièrement utilise pour l'étude de la réponse de système à des signaux très irréguliers comme ceux issus d’un séisme.
L’impulsion de Dirac \(\delta(t)\) est une fonction idéalisée qui modélise une excitation de très courte durée mais de quantité de mouvement finie. Elle est mathématiquement définie par deux propriétés fondamentales :
$$ \delta(t) = 0 \text{ pour } t \ne 0, \quad \int_{-\infty}^{\infty} \delta(t) \, dt = 1 $$
Lorsqu’un système est soumis à une impulsion unitaire \(\delta(t)\), il réagit par une notée \(h(t)\), qui représente le comportement du système dans le temps après cette excitation instantanée.
Si l’on connaît \(h(t)\), on peut déterminer la réponse du système à une force externe arbitraire \(f(t)\) grâce à un produit de convolution temporel :
$$ x(t) = \int_{0}^{t} h(t - \tau) f(\tau) \, d\tau $$
Cette formule signifie que l’on considère la force \(f(t)\) comme une somme continue d’impulsions différentielles \(f(\tau) \, d\tau\), chacune produisant une réponse \(h(t - \tau)\), que l’on additionne sur tout l’intervalle de temps.
Dans le cas d'un système à 1DDL avec amortissement, la réponse impulsionnelle \(h(t)\) peut être déterminée analytiquement. Supposons que le système est initialement au repos, et que l’on applique une impulsion unitaire à \(t = 0\). L’équation devient :
$$ m \ddot{x}(t) + c \dot{x}(t) + k x(t) = \delta(t) $$
La solution correspond à la fonction de réponse impulsionnelle, qui dépend du rapport d’amortissement \(\zeta = \frac{c}{2\sqrt{km}}\). Pour le cas sous-amorti (\(0 < \zeta < 1\)), la réponse impulsionnelle est :
$$ \boxed{h(t) = \frac{1}{m \omega_d} e^{-\zeta \omega_0 t} \sin(\omega_d t) \cdot u(t)} $$
avec : \(\omega_0 = \sqrt{\frac{k}{m}}\) la pulsation propre, \(\omega_d = \omega_0 \sqrt{1 - \zeta^2}\) la pulsation amortie, \(u(t)\) est la fonction échelon de Heaviside (c'est à dire que \(h(t) = 0\) pour \(t <0\) car le signal est causal...)
Implémentation sous MATLAB
Une première implémentation de la méthode par décomposition impulsionnelle que nous avons réalisés sur MATLAB consiste à utiliser la fonction integral pour effectuer l’intégrale de convolution de manière explicite (cf. code en annexe).
Dans cette méthode, on considère que l’on souhaite calculer la réponse \(x(t)\) à un instant donné \(t\). On définit une fonction anonyme dans MATLAB correspondant à l’intégrande \(h(t - \tau) \cdot f(\tau)\), et on utilise la fonction integral pour évaluer l’intégrale entre \(0\) et \(t\).
On répète cette opération pour chaque valeur de \(t\) (discrétisé sur l’intervalle étudié avec une boucle for) afin d’obtenir le vecteur complet de la réponse. Cette méthode est particulièrement utile lorsque la fonction d’excitation \(f(t)\) est donnée sous forme analytique, ou lorsqu’elle est définie point par point mais suffisamment régulière pour permettre une interpolation continue. Toutefois, l’application de cette méthode devient plus complexe lorsque l’excitation \(f(t)\) est issue d’un signal aléatoire, comme une accélération sismique. En effet, MATLAB a besoin d’une fonction continue \(f(\tau)\) pour effectuer l’intégration. Or, un signal aléatoire n’est généralement donné que par un vecteur de données discrètes (et n'est donc pas continu). Une possibilité est donc d'interpoler ce vecteur à l’aide d’une fonction comme interp1.
Cela est possible mais cela ajoute cette étape supplémentaire (et coûteuse en terme de calcul et de précision) d'interpolation du signal, dans le cas d'un signal aléatoire. C'est la raison pour laquelle nous n'avons finalement pas retenu cette méthode d'implémentation pour notre code final.
Nous avons donc finalement choisi d'utiliser la fonction conv (déjà incluse dans MATLAB) qui permet de réaliser cette opération de manière discrète. L'avantage de cette seconde implémentation est qu'elle permet aussi bien de traiter un signal défini par une fonction continue (une excitation harmonique par exemple) qu'un signal aléatoire discontinu tel que celui mesuré lors d'un séisme.
La première étape consiste là aussi à discrétiser le système. Ensuite, on applique la convolution discrète entre \(h(t)\) et \(f(t)\) (où \(f(t)\) est le signal correspondant à l'excitation). Cette opération revient à simuler la superposition des mini-réponses à chaque échantillon du signal d’entrée. Cependant, il est important de multiplier le résultat par le pas de temps \(\Delta t\) pour obtenir une approximation correcte de l’intégrale de convolution continue. Le signal résultant est généralement plus long que le signal initial (somme des longueurs moins une), ce qui impose éventuellement de tronquer ou d'ajuster la taille du vecteur de sortie pour correspondre à celle du signal temporel d'entrée (nous avons initialement rencontré cette difficulté).
Dans le cas où le signal d’entrée \(f(t)\) est aléatoire, plusieurs difficultés peuvent apparaître. D’abord, un signal aléatoire peut contenir des hautes fréquences parasites ou des discontinuités, ce qui nécessite souvent un prétraitement : filtrage passe-bas, suppression de la moyenne, ou lissage du signal.
Une autre difficulté réside dans le choix de la durée de la réponse impulsionnelle. En théorie, \(h(t)\) s’étend à l’infini (dans le cas sans amortissement), mais en pratique, on la tronque à une durée où l’amplitude est devenue négligeable (en général quelques multiples de la constante de temps \(1/\zeta \omega_0\)). Un mauvais choix peut provoquer des artefacts en bord de signal ou des effets de troncature non physiques.
Décomposition indicielle
Principe théorique
La décomposition indicielle, contrairement à la décomposition impulsionnelle, qui repose sur la réponse à une impulsion, s’appuie sur la réponse à un échelon unitaire appliqué sur un petit intervalle de temps.
L’idée est la même que pour la décomposition impulsionnelle : on représente l’excitation quelconque \(f(t)\) comme une somme pondérée de réponses à des fonctions échelon définies sur des intervalles élémentaires. Si l’on discrétise le temps avec un pas \(\Delta t\), on peut approximer l’excitation \(f(t)\) par une somme de fonctions constantes par morceaux. Cette méthode nécessite de connaître la réponse du système à un échelon unitaire. Celle-ci est bien connue pour un système à 1DDL amorti :
$$\boxed{ g(t) = \frac{1}{k} \left(1 - \frac{1}{\sqrt{1 - \zeta^2}} e^{-\zeta \omega_0 t} \sin(\omega_d t + \phi)\right)}$$
avec \(\omega_0 = \sqrt{k/m}\) la pulsation propre, \(\zeta = \frac{c}{2 \sqrt{km}}\) le facteur d’amortissement, \(\omega_d = \omega_0 \sqrt{1 - \zeta^2}\) la pulsation amortie et \(\phi = \arccos(\zeta)\).
Le signal résultant est alors :
$$\boxed{x(t) = f(0)g(t) + \int_0^t \frac{\text{d}f(\tau)}{\text{d}\tau}g(t-\tau)\text{d}\tau}$$
Cette méthode, contrairement à la méthode précédente, fait directement intervernir la dérivée de \(f\). On peut dors et déjà supposer (et cela sera confirmé lors de l'implémentation du codes) que cela va poser des difficultés dans le cas de signaux aléatoires discontinus.
La solution que nous avons retenue dans ce cas, est d'interpoler le signal par une fonction \(\mathcal{C}^1\) en utilisant la fonction interp1 de MATLAB.
Méthode numérique d'Euler
Principe théorique et implémentation
Pour appliquer la méthode d’Euler, on réécrit l'équation du système (une équation d'ordre 2) forme d’un système d’équations différentielles du premier ordre :
$$ \begin{cases} \dot{x}(t) = v(t) \\ \dot{v}(t) = \dfrac{1}{m} \left( f(t) - c v(t) - k x(t) \right) \end{cases} $$
La méthode d’Euler consiste alors à approximer la dérivée par une différence finie sur un pas de temps \(\Delta t\) :
$$ \begin{cases} x_{n+1} = x_n + \Delta t \cdot v_n \\ v_{n+1} = v_n + \Delta t \cdot \left( \dfrac{1}{m} (f_n - c v_n - k x_n) \right) \end{cases} $$
Pour implémenter cette méthode en MATLAB, nous avons initialisé des vecteurs de solution : des vecteurs pour \(x\), \(v\), avec des conditions initiales données (par exemple \(x_0 = 0\), \(v_0 = 0\)). Ensuite, avec une boucle, on parcourt chaque instant \(t_n\) et on applique les formules d’Euler pour obtenir \(x_{n+1}\) et \(v_{n+1}\).
La méthode d’Euler fut relativement simple à implémenter, cependant nous avons pu constater que sa précision dépendait fortement du choix du pas de temps \(\Delta t\) (cf. paragraphes suivants). Pour un système oscillant, des pas trop grands peuvent provoquer une instabilité numérique, c’est-à-dire des solutions divergentes ou non physiques. Cela est encore plus critique si le système est peu amorti.
Enfin, il y a une difficulté supplémentaire pour les signaux aléatoires : les variations rapides peuvent nécessiter un pas de temps très petit pour "capter" correctement les variations très rapides du signal. Cela allonge considérablement le temps de calcul. Pour ce type de signaux, nous avons finalement choisi d'utiliser des solveurs intégrés MATLAB comme ode45.
Comparaison des différentes méthodes et étude de l'influence de différents paramètres
Étude de l'influence de l'amortissement
Au début de l’étude, les deux courbes issues de la décomposition impulsionnelle et de la décomposition indicielle présentaient une forme parfaitement identique, mais avec un léger décalage dans le temps. Ce décalage est dû à un problème de discrétisation temporelle dans le calcul de la dérivée \(df/dt\). En effet, dans la méthode indicielle, la dérivée est souvent approchée par une différence finie de type avant ou arrière, ce qui introduit un retard ou une avance artificielle dans la réponse. Ce décalage est typique des approximations numériques non centrées, et peut être corrigé en utilisant des schémas plus précis (différence centrée) ou en recadrant temporellement la réponse. Cela montre l’importance de bien choisir les méthodes de dérivation et de convolution pour garantir la cohérence temporelle des réponses simulées.
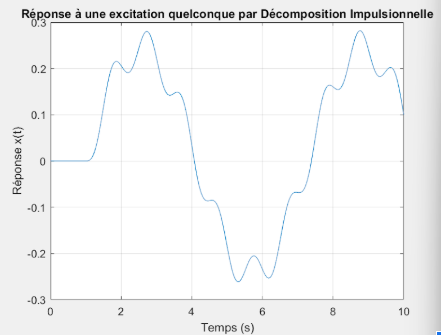Résultat obtenu par décomposition impulsionnelle 
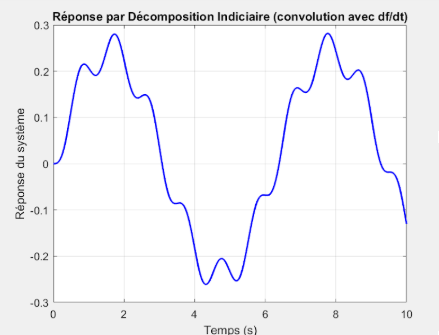Résultat obtenu par décomposition indicielleDécalage temporel présent dans la première version du code
Paramètres:
- m=1 kg
- k=6 N/m
- c=0.01 Ns/m (amortissement très faible)
- dt = 0.01
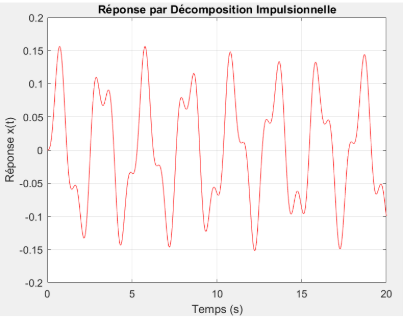Résultat obtenu par décomposition impulsionnelle 
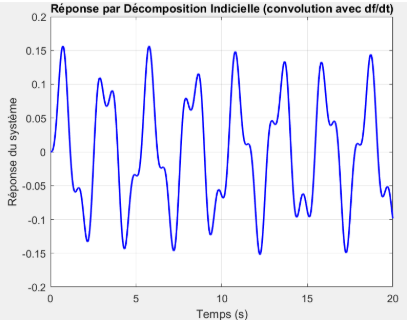Résultat obtenu par décomposition indicielleComparaison décomposition impulsionnelle/indicielle pour un premier jeu de paramètres
Comme attendu, les courbes obtenues sont les mêmes pour la décomposition indicielle et la décomposition impulsionnelle.
Il s’agit d’une courbe périodique montrant une forme complexe, avec des pics irréguliers (non parfaitement sinusoïdaux). L'amplitude maximale reste relativement constante (+0.15 à -0.15), sans décroissance notable, cela est dû à un amortissement très faible (quasi-négligeable).
La réponse présente des oscillations non symétriques (des pics plus prononcés et d'autres plus plats), ce qui est typique de la convolution d'une excitation sinusoïdale dérivée (\(df/dt\)) avec une fonction indicielle amortie. Le signal reste borné sans tendance à la divergence, confirmant un système stable.
Il s'agit de la réponse transitoire d'un système légèrement amorti à une excitation périodique, obtenue par une convolution numérique. Le faible amortissement entraîne une réponse oscillante durable, et la convolution avec la dérivée du signal d'entrée (\(df/dt\)) donne une forme de réponse complexe et légèrement déphasée par rapport à l'entrée.
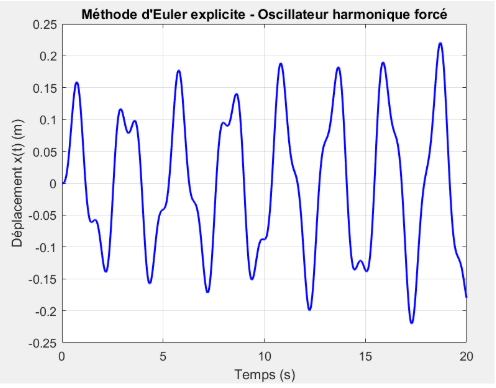Méthode d'Euler (même fonction et mêmes paramètres)
La méthode d'Euler donne la solution directe de l'équation différentielle, donc une réponse plus fidèle au système physique mais avec une approximation numérique. La décomposition indicielle donne une solution basée sur le principe de superposition, en utilisant la réponse indicielle du système. La forme de la courbe est influencée par la convolution avec la dérivée du signal d'entrée (\(df/dt\)), ce qui explique les irrégularités et les "sauts" dans la réponse. Les tendances générales sont similaires : un système faiblement amorti qui oscille sous excitation sinusoïdale.
Les deux courbes montrent bien la dynamique d'un oscillateur harmonique faiblement amorti excité par une force sinusoïdale. La méthode d'Euler donne une approximation numérique directe, tandis que la décomposition indicielle met en lumière l'effet de la forme de l'excitation et du filtrage induit par le système.
Nouveau jeu de paramètres (très fort amortissement):
- m=1 kg
- k=6 N/m
- c=10 Ns/m
- dt = 0.01
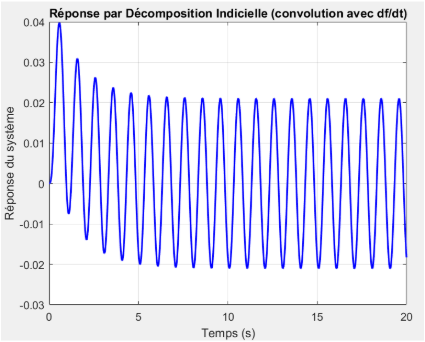Décomposition indicielle 
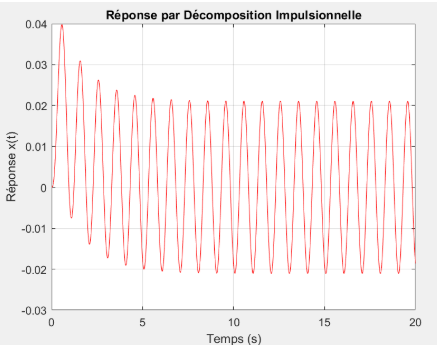Décomposition impulsionnelle 
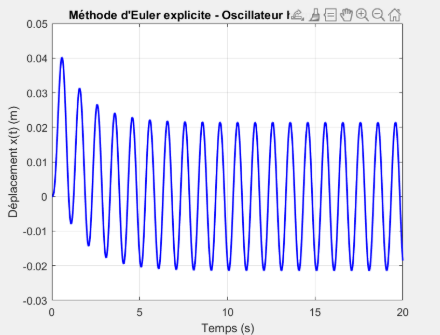Méthode d'Euler
Comparaison des trois méthodes de résolution (effet de l'amortissement)
Nous pouvons observer que les 3 courbes sont identiques avec un coefficient d’amortissement assez grand: L’oscillation démarre avec une amplitude autour de 0.04 m, puis diminue rapidement pour se stabiliser autour de \(±0.02m\). La courbe montre une forte atténuation des premières oscillations, avec un régime permanent rapidement atteint. La fréquence reste stable, mais l’amplitude diminue fortement au début, caractéristique d’un fort amortissement. La forte valeur de \(c=10\) impose un amortissement très important, ce qui supprime rapidement les effets transitoires.
L'oscillation persiste grâce à la force sinusoïdale externe, mais avec une amplitude fortement réduite et stabilisée rapidement.
Nous prendrons \(c=0.1\) pour la suite des études.
Étude de l'influence de \(k\) et \(m\) (donc de \(\omega_p\))
Essayons maintenant avec une constante de raideur relativement élevée: \(k=30\).
Dans cette configuration avec une masse de \(1 kg\), une raideur de \(30 N/m\) et un faible amortissement de \(0.1 N·s/m\), les différentes méthodes donnent des résultats globalement cohérents, mais avec des différences significatives selon la stabilité et la précision numérique.
La méthode d’Euler explicite montre une réponse oscillatoire dont l’amplitude croît continuellement dans le temps, ce qui indique une instabilité numérique. Cette instabilité est due à la nature explicite du schéma d’intégration et à une accumulation d’erreurs à chaque pas de temps. Bien que la fréquence soit correcte, l’amplitude dépasse 1.5 m, ce qui n’est pas compatible avec un système linéaire faiblement amorti soumis à une excitation sinusoïdale modérée.
À l’inverse, la réponse obtenue par décomposition indicielle reste stable, avec des oscillations modérées et une amplitude bornée. Le signal montre des battements caractéristiques d’un système soumis à une excitation proche de sa fréquence propre, avec une modulation régulière de l’amplitude. Cette méthode, basée sur la convolution de la réponse indicielle avec la dérivée de l’excitation, est plus fidèle au comportement physique attendu et plus robuste numériquement.
Enfin, la courbe représentant la réponse obtenue par décomposition impulsionnelle (en rouge) est identique à celle obtenue par décomposition indicielle. Cela confirme que les deux approches sont mathématiquement équivalentes pour les systèmes linéaires invariants dans le temps, à condition de bien respecter la convolution causale. Les deux courbes montrent le même comportement oscillatoire, les mêmes modulations d’amplitude et une stabilité parfaite sur toute la durée d’observation.
Ainsi, les méthodes par décomposition (indicielle ou impulsionnelle) sont fiables et précises, tandis que la méthode d’Euler explicite peut devenir instable dans certains cas. Il est donc essentiel de choisir la méthode de résolution en fonction des propriétés du système et du niveau de précision requis.
Cf. Figures en page 14
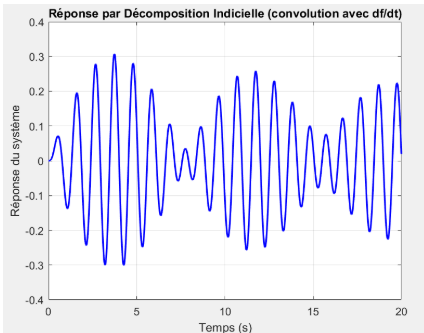Décomposition indicielle 
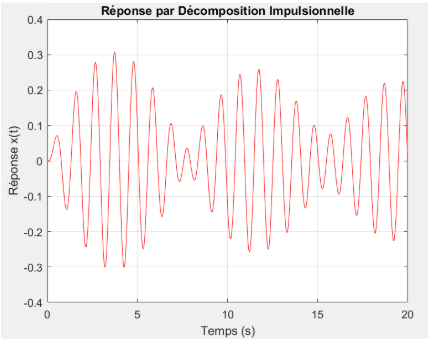Décomposition impulsionnelle 
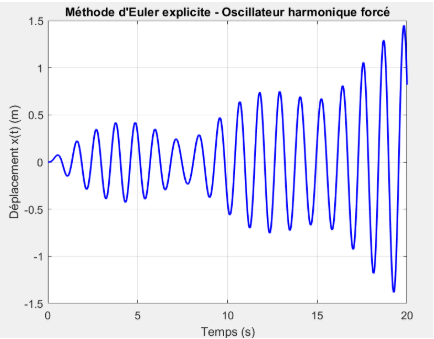Méthode d'Euler
Comparaison des trois méthodes de résolution (effet de \(\omega_p\))
Remplaçons la valeur de \(k\), elle est maintenant égale à 0,5.
Dans cette nouvelle simulation, la raideur \(k\) du ressort est fortement réduite à une valeur de \(0.5 N/m\), ce qui modifie profondément le comportement du système. Une faible raideur implique une pulsation propre très basse, ce qui rend le système beaucoup plus lent à réagir aux sollicitations extérieures et plus sensible à l’amplitude des forces appliquées. Cela se reflète clairement dans les trois courbes obtenues.
La réponse obtenue par la méthode d’Euler explicite montre un déplacement dont la forme est parfaitement cohérente avec une réponse physique. L’oscillation est lente, avec une fréquence bien plus faible que dans les cas précédents, et l’amplitude atteint environ \(±0.3 m\). La forme de l’onde est asymétrique avec des modulations d’amplitude visibles. La méthode semble stable, sans dérive ni amplification non physique.
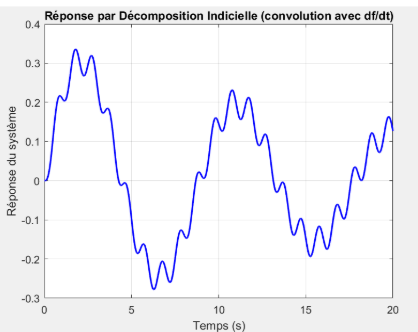
La réponse par décomposition indicielle (convolution avec la dérivée de la force) montre une courbe très proche de celle obtenue par Euler. On retrouve exactement la même fréquence lente, les mêmes creux et pics au même moment, avec une amplitude identique. Cela montre que les deux méthodes convergent vers la même solution, ce qui confirme la fiabilité numérique du schéma même en régime lent et faiblement raide.
La courbe obtenue par décomposition impulsionnelle, représentée en rouge, est elle aussi très proche des deux autres. La forme générale de la courbe, les pics, la fréquence et l’amplitude sont les mêmes. Seules de très légères différences apparaissent dans la finesse de certaines oscillations, ce qui peut s’expliquer par la discrétisation temporelle ou la méthode de calcul utilisée pour la convolution. En conclusion, lorsque k est faible, le système réagit lentement avec de grandes amplitudes. Les trois méthodes donnent ici des résultats parfaitement compatibles.
Cela montre que dans les cas de faible raideur, toutes les approches (intégration numérique, convolution indicielle ou impulsionnelle) permettent de reproduire fidèlement la dynamique du système, à condition que le pas de temps soit suffisamment petit pour suivre la lenteur du mouvement.
Cf. Figures en page 15
Décomposition indicielle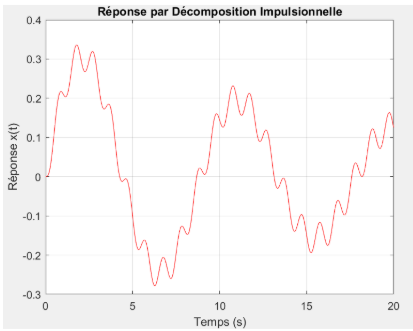 
Décomposition impulsionnelle 
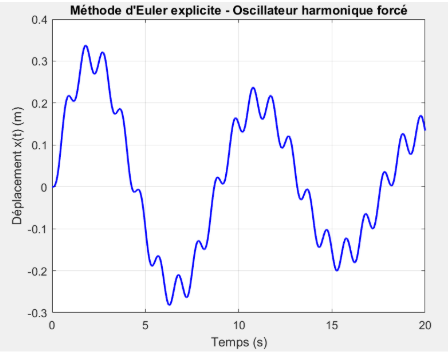Méthode d'Euler
Comparaison des trois méthodes de résolution (effet de \(\omega_p\))
Reprenons \(k=6\) pour le reste de l’étude.
Étudions maintenant l’impact de la masse. Nous allons dans un premier temps prendre une masse importante, \(m=200kg\).
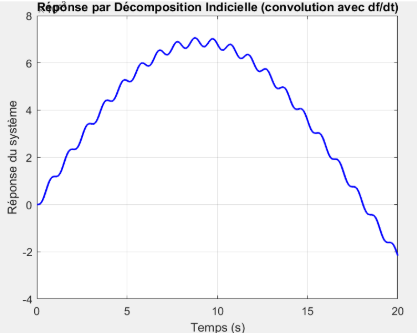Décomposition indicielle 
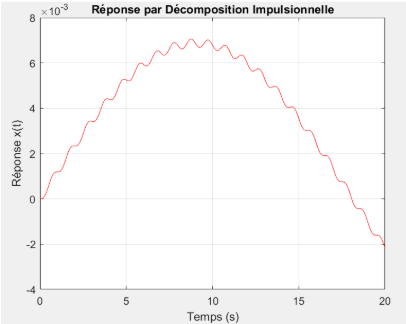Décomposition impulsionnelle 
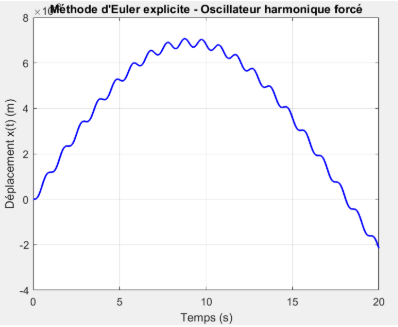Méthode d'Euler
Comparaison des trois méthodes de résolution (effet de \(\omega_p\))
Dans cette configuration, la masse du système est augmentée à une valeur très élevée, \(m=200 kg\), tandis que la raideur est maintenue à \(k=6 N/m\). Cette masse importante a pour effet de diminuer fortement la pulsation propre du système, ce qui se traduit par une réponse très lente, peu oscillatoire et globalement amortie.
Les trois courbes obtenues par les différentes méthodes Euler explicite, décomposition indicielle, et décomposition impulsionnelle présentent exactement la même forme : une évolution en cloche, très progressive. Le déplacement commence à zéro, croît lentement jusqu’à un maximum autour de \(t=10 s\), puis redescend symétriquement vers une valeur négative. Cette symétrie et cette lenteur indiquent que l’inertie domine largement le comportement dynamique, rendant la réponse très amortie et peu sensible aux variations rapides de la force excitatrice.
L’amplitude maximale atteinte est très faible, de l’ordre de quelques millimètres. Cela confirme que malgré une excitation sinusoïdale, la masse très élevée empêche une réponse rapide du système. L’effet des forces est "lissé" par l’inertie, et toute variation rapide est fortement atténuée.
Les trois méthodes numériques donnent ici des résultats parfaitement identiques : même courbe, même amplitude, même forme. Cela démontre que lorsque le système est dominé par la masse et que les variations sont lentes, toutes les approches convergent vers une même solution, fiable et précise.
En conclusion, l’augmentation de la masse ralentit fortement la réponse du système, diminue l’amplitude des oscillations et conduit à une dynamique très peu vibratoire. Dans ce cas, toutes les méthodes étudiées restent précises et cohérentes, ce qui permet une validation croisée robuste.
Cf. Figures en page 17
Étude de l'influence du pas de temps
Nous reprenons \(m=1\).
Étudions maintenant l’impact de la discrétisation du temps avec \(tmax\) fixé à \(20s\). Nous avons déjà vue qu’en était il lorsque \(dt\) était assez petit (0.01), étudions maintenant le cas pour \(dt = 1\) (volontairement "trop" grand).
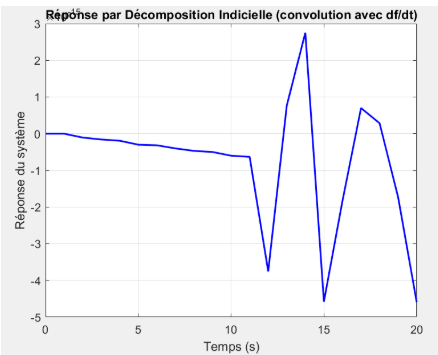Décomposition indicielle 
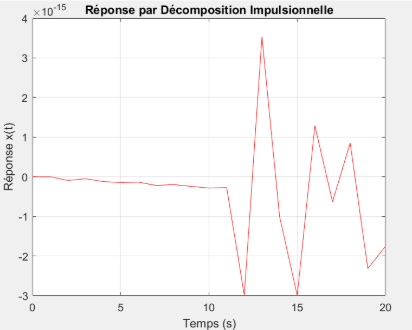Décomposition impulsionnelle 
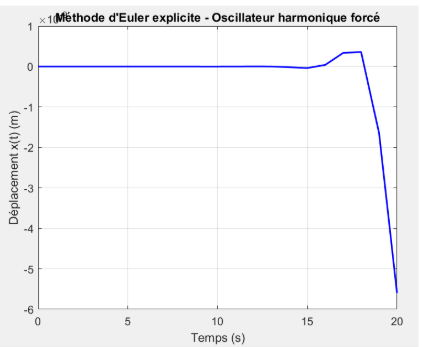Méthode d'Euler
Comparaison des trois méthodes de résolution (effet du pas de discrétisation)
Dans cette dernière configuration, la masse est fixée à \(m=1kg\) comme dans les cas de référence, mais le pas de temps a été fortement augmenté à \(dt=1s\), ce qui correspond à une discrétisation très grossière de l’évolution temporelle. Cette modification a un impact majeur sur la précision numérique et la stabilité des trois méthodes.
La courbe obtenue par la méthode d’Euler explicite montre une évolution erratique, non physique, avec un comportement instable et des valeurs extrêmes qui apparaissent brutalement en fin de simulation. Le déplacement reste proche de zéro jusqu’à environ 18 secondes, puis chute brutalement à une valeur d’environ -6. Cela indique que le schéma numérique est devenu instable à cause du pas de temps trop grand.
L’intégration accumule de fortes erreurs et devient incapable de suivre correctement la dynamique réelle du système. La courbe de la méthode par décomposition indicielle (convolution avec df/dt) présente également une dégradation de la qualité numérique. La réponse du système devient irrégulière, avec de grandes variations entre les points, qui semblent davantage liées aux erreurs de calcul qu’au comportement physique attendu. L’aspect saccadé et l’amplitude incohérente sont typiques d’un échantillonnage trop faible du signal.
Enfin, la courbe obtenue par décomposition impulsionnelle montre un résultat quasi nul pendant toute la durée de la simulation, avec des pics très discrets de l’ordre de \(10^{-15}\), ce qui correspond probablement à des erreurs numériques proches du bruit machine. Cela indique que cette méthode devient inefficace pour un pas de temps aussi large, car la convolution n’est plus capable de capturer les variations de la réponse impulsionnelle à cette échelle.
En conclusion, une discrétisation du temps trop grossière (\(dt=1 s\)) dégrade fortement la qualité des trois méthodes. La méthode d’Euler explicite devient instable, la méthode indicielle perd en précision, et la méthode impulsionnelle devient silencieuse ou bruitée. Ces résultats confirment l’importance du choix du pas de temps pour assurer la stabilité et la fidélité de la simulation numérique d’un système dynamique. Un petit \(dt\) est donc, comme attendu, essentiel pour bien capturer les variations rapides et garantir la convergence des solutions.
Cf. Figures en page 19
Conclusion
L’étude des réponses d’un oscillateur harmonique forcé à l’aide de différentes méthodes numériques (Euler explicite, décomposition indicielle et impulsionnelle) a permis d’analyser en détail l’influence des paramètres physiques du système (raideur \(k\), masse \(m\), amortissement \(c\)) ainsi que celle de la discrétisation temporelle dt sur la qualité et la stabilité des résultats obtenus.
Lorsque la raideur \(k\) est faible, le système devient lent, les oscillations sont de faible fréquence et de grande amplitude. Les trois méthodes donnent des résultats cohérents et précis à condition de conserver un pas de temps suffisamment fin. À l’inverse, pour une raideur plus élevée, la fréquence naturelle augmente, ce qui demande une résolution temporelle plus adaptée pour éviter les erreurs d’échantillonnage.
La masse m a également un rôle déterminant : une masse élevée ralentit la réponse, amortit naturellement les oscillations et produit des déplacements de faible amplitude. Au contraire, une masse très faible rend le système très rapide et réactif, ce qui peut entraîner des oscillations de grande amplitude et nécessite une discrétisation fine pour bien suivre les variations rapides du mouvement.
Le coefficient d’amortissement c agit sur la durée du régime transitoire. Un amortissement faible permet aux oscillations de se maintenir longtemps, voire de résonner si l’excitation est proche de la fréquence propre. Un amortissement élevé atténue rapidement les oscillations et stabilise le système. Les méthodes numériques se comportent bien dans les deux cas, mais leur stabilité peut varier selon les valeurs combinées de \(c\), \(m\) et \(k\).
Enfin, la discrétisation temporelle joue un rôle crucial. Un pas de temps trop grand (\(dt=1\)) détériore fortement les résultats. La méthode d’Euler devient instable, les convolutions perdent leur précision, et l’ensemble des courbes ne reflète plus le comportement physique réel du système. En revanche, un pas de temps suffisamment petit (\(dt=0,01\)) assure une bonne convergence des trois méthodes, qui produisent alors des résultats fiables et superposables.
Ainsi, pour simuler fidèlement un système dynamique, il est essentiel d’adapter la méthode numérique et le pas de temps aux caractéristiques physiques du système. Les méthodes par décomposition (indicielle ou impulsionnelle) sont robustes et précises, mais nécessitent une bonne résolution temporelle. La méthode d’Euler explicite peut être performante pour des régimes simples, mais elle devient instable en cas de mauvaise discrétisation. Cette étude met en évidence l’importance du couplage entre modélisation physique et choix numérique pour garantir des résultats fiables.
Application à l’étude des TMD
Historique et principe de fonctionnement
Les amortisseurs de masse accordés (TMD) sont des dispositifs conçus pour réduire les vibrations dans les structures, notamment les gratte-ciels, en contrebalançant les oscillations causées par le vent ou les tremblements de terre. Ils améliorent le confort des occupants en limitant les mouvements et surtout protègent l'intégrité structurelle contre l'usure. Leur importance est particulièrement marquée pour les tours élancées, où les vibrations peuvent causer nausées ou dommages, comme illustré par le pendule géant de Taipei 101 (7).
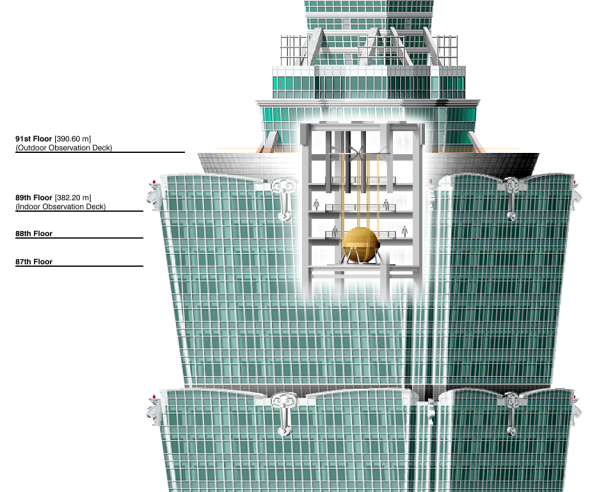Schéma du TMD de Taipei 101 
La masse du TMDIllustrations du TMD de Taipei 101
Les TMD ont été initialement développés par Herman Frahm au début du 20e siècle pour des systèmes mécaniques, avec des applications initiales pour stabiliser les coques de navires. Les travaux théoriques d'Ormondroyd et Den Hartog dans les années 1920 et 1940 ont jeté les bases de leur utilisation dans les bâtiments. La chute du pont de Tacoma en 1940 fut l’un des événements qui déclencha un véritable intérêt pour ces dispositifs. Grâce au progrès des matériaux et de la science, cette période a également vu la naissance de structures de plus en plus audacieuses (7). Les années 1970 ont vu leur adoption dans des gratte-ciels comme le John Hancock Center et le Citicorp Center pour gérer les oscillations dues au vent, suivies par des innovations comme les systèmes actifs dans le bâtiment Kyobashi Seiwa à Tokyo en 1989. L'évolution s'est poursuivie avec des designs avancés, tels que le pendule de 660 tonnes de Taipei 101, montrant une transition des systèmes passifs aux systèmes actifs capables de s'adapter en temps réel.
Modélisation du système
Le choix de modélisation de cette partie s'appuie en grande partie sur la modélisation proposée par (6).
Pour dissiper efficacement l’énergie causée par une vibration il faut que ce système soit à masse accordée. Cela signifie que le système masse-ressort (qui modélise de TMD), doit posséder une fréquence propre identique à celle de la structure (la tour), sinon le TMD est sans utilité. Le choix de la raideur \(k\) et de la masse \(m\) du TMD ne sont donc pas anodins : ils doivent être soigneusement choisis pour que le TMD ait la même fréquence propre que la tour. Dans le cas de la tour Taipei 101, la masse du TMD (cf. figure 11.b) est de \(660\) t.
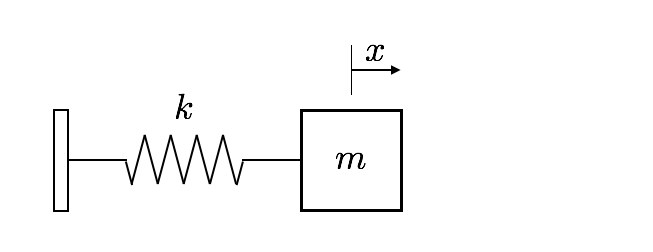Modélisation du TMD par un système masse-ressort (1DDL) 
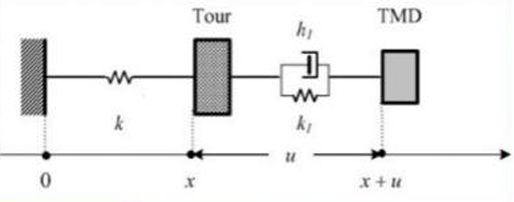Modélisation du système Tour+TMD (2DDL)Choix de modélisation du système
Le système (Tour + TMD) peut alors être modélisé de la manière suivante. Contrairement aux systèmes étudiés lors des parties précédentes, il s'agit d'un système à deux degrés de libertés. Une étude théorique des systèmes à 2DDL s'avère donc nécessaire avant de poursuivre l'étude de l'influence du TMD sur les oscillations de la structure.
Étude théorique des systèmes à 2DDL
Pour étudier le comportement dynamique de systèmes à 2 degrés de liberté, on utilise couramment la méthode de Lagrange, qui permet plus généralement d'étudier des systèmes à N degrés de liberté (5).
Cette méthode consiste à introduire deux coordonnées généralisées \(q_1(t)\) et \(q_2(t)\), à exprimer l’énergie cinétique \(T\) et l’énergie potentielle \(V\) en fonction de ces variables, puis à former le lagrangien \(\mathcal{L} = T - V\). On applique ensuite les équations de Lagrange pour chaque coordonnée :
$$ \frac{d}{dt} \left( \frac{\partial \mathcal{L}}{\partial \dot{q}_i} \right) - \frac{\partial \mathcal{L}}{\partial q_i} = 0 \quad \text{pour } i = 1, 2. $$
On obtient alors un système d’équations différentielles couplées, que l’on peut linéariser et mettre sous forme matricielle (5).
$$ M \ddot{\mathbf{q}} + K \mathbf{q} = 0, $$
où \(M\) et \(K\) sont respectivement les matrices de masse et de raideur. En cherchant des solutions harmoniques, on détermine les fréquences propres et les modes propres, qui décrivent comment le système vibre naturellement (et correspondent respectivement aux valeurs propores et vecteurs propres de cette matrice).
Étude théorique du système
Le système Tour+TMD est ainsi modélisé par deux oscillateurs unidimensionnels couplés mis en mouvement par la force extérieure \(f_0(t)\).
Le premier oscillateur (la tour) est modélisé par une masse \(m\) soumise à la force de rappel élastique \(f_{elas}=-kx\) et à la force de frottement fluide \(\phi = -h\dot{x}\).
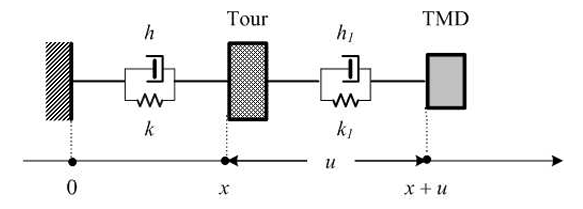Modèle du système
Le second oscillateur (le TMD) est modélisé par une masse \(m_1\) soumise à la force de rappel élastique \(f_1 = -k_1 u\) et à la force de frottement fluide \(\phi_1 = -h\dot{u}\).
Le détails de l'étude théorique du système Tour+TMD sort du cadre de ce projet (cf. référence (6)). On admet donc dans la suite que ce système suit les équations suivantes :
\[ \begin{cases} (1 + \alpha)\, \ddot{x} + \alpha\, \ddot{u} + \omega_0^2 x = a_0(t) & \text{avec } \alpha = \dfrac{m_1}{m},\ \omega_0 = \sqrt{\dfrac{k}{m}},\ a_0(t) = \dfrac{f_0(t)}{m} \\ \\ \ddot{x} + \ddot{u} + 2\eta_1 \omega_1 \dot{u} + \omega_1^2 u = 0 & \text{avec } \omega_1 = \sqrt{\dfrac{k_1}{m_1}},\ \eta_1 = \dfrac{h_1}{2 \sqrt{k_1 m_1}} \end{cases} \]
On s'intéresse à la réponse du système à l'excitation (harmonique par exemple pour simuler l'action du vent sur la tour) \(a_0(t) = \Re(A_0 \exp(i\omega t))\) en notation complexe. Les amplitudes complexes de \(u(t)\), \(a_0(t)\) et \(x(t)\) sont notées respectivement \(\underline{U}\), \(\underline{A}\) et \(\underline{X}\). On pose enfin \(\beta = \frac{\alpha}{\omega_0}\) \(\left(\beta = \sqrt{\alpha \frac{k}{k_1}}\right)\).
Après quelques calculs, on trouve $$\boxed{H_1(z) = \frac{z^2}{-z^2+2i\eta_1\beta z+\beta^2}}$$ (il s'agit d'un filtre passe haut d'ordre 2). Le TMD a donc bien pour effet les oscillations "rapides" correspondant aux hautes fréquences.
\[ H_1(z) = \frac{\underline{U}}{\underline{X}} \]
De même, la fonction de transfert $$H_2(z) = \dfrac{\underline{\ddot{X}}}{\underline{A_0}} = \boxed{\dfrac{z^2}{\left(1 + \alpha + \alpha H_1\right) z^2 - 1}}$$
Étude de l'effet des différents paramètres
Le tracé du module (gain) de \(H_2\) en fonction de \(\frac{\omega}{\omega_0}\) pour différentes valeurs de \(\eta_1\) (0.1, 0.3 et 0.6) a été réalisé avec le code MATLAB (cf. annexe 7.7) et donne le résultat suivant :
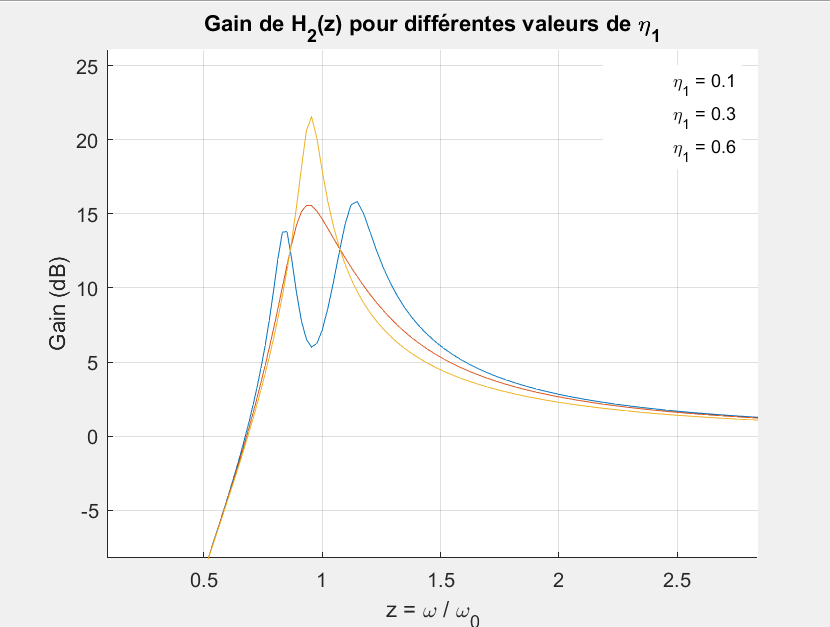Gain de \(H_2\) pour différentes valeurs de \(\eta_1\)
On rappelle que \(\eta_1 = \dfrac{h_1}{2 \sqrt{k_1 m_1}}\). Un raisonnement fondé sur l’analyse dimensionnelle permet d’interpréter les faibles valeurs de \(\eta_1\) comme correspondant à un amortissement relativement important du TMD, c’est-à-dire que \(\sqrt{k_1 m_1} \gg h_1\). À l’inverse, lorsque \(\eta_1 \geq 1\), l’action du TMD devient inefficace, ce que confirment les courbes de gain.
En effet, la courbe jaune (correspondant à \(\eta_1 = 0{,}6\)) présente un profil de gain similaire à ceux observés dans les cas sans TMD sous excitation harmonique. En revanche, la courbe bleue (\(\eta_1 = 0{,}1\)) illustre l’effet bénéfique du TMD, avec une dissipation d’énergie plus efficace qui se traduit par deux pics de gain atténués.
Conclusion
Ce travail avait pour objectif d’étudier la réponse dynamique d’un bâtiment soumis à une excitation quelconque, en analysant l’influence des paramètres mécaniques (masse, raideur, amortissement) ainsi que du pas de temps sur le comportement vibratoire. Nous avons comparé plusieurs méthodes numériques de résolution : la méthode d’Euler explicite, la décomposition indicielle et la décomposition impulsionnelle.
L’ensemble des simulations a mis en évidence des phénomènes caractéristiques de la dynamique des structures, tels que la résonance et l'existence de modes propres, l’amortissement ou encore l’instabilité liée à une discrétisation trop grossière. Ces comportements ont été interprétés à la lumière des notions fondamentales de fréquence propre, de réponse en régime forcé et de stabilité numérique.
Les codes développés sous MATLAB nous ont permis de tester ces différentes méthodes de manière visuelle. Ils ont facilité la mise en œuvre des simulations et ont permis de générer des courbes claires, révélant les effets directs des paramètres étudiés. Leur utilisation a également mis en évidence les limites de certaines approches, comme l’instabilité d’Euler explicite pour de grands pas de temps.
Enfin, ce projet nous a permis de comprendre et de modéliser le fonctionnement des TMD, ainsi que d’évaluer leur intérêt dans la réduction des vibrations. Il nous a offert l’opportunité d’approfondir notre compréhension des phénomènes vibratoires au sein d’un système linéaire simple, et d’illustrer concrètement l’influence de chacun des paramètres dynamiques.
Avec un peu plus de temps, ce travail aurait pu être enrichi par des expérimentations pratiques, permettant de confronter les résultats théoriques aux observations réelles et de valider la pertinence des modèles utilisés.
Annexes
Étude de l'influence de \(\xi\) sur le phénomène de résonance (Python)
import numpy as np
import matplotlib.pyplot as plt
def amplitude_stationnaire_xi(xi, F0, m, omega_0, omega):
Q = 1 / (2 * xi)
zeta = xi
num = F0 / m
denom = np.sqrt((omega_0**2 - omega**2)**2 + (2 * zeta * omega_0 * omega)**2)
return num / denom
# Comparaison pour différentes valeurs de xi
xi = [1, 0.5, 0.1, 0.025] # xi = 1 (très amorti), xi = 0 (pas amorti)
omega_0 = 2 * np.pi * 1 # fréquence propre = 1 Hz
frequence = np.linspace(0.1, 2 * omega_0, 500)
F0 = 1
m = 1
plt.figure(figsize=(12, 8))
for xi in xi:
amplitudes = amplitude_stationnaire_xi(xi, F0, m, omega_0, frequencies)
plt.plot(frequence / (2 * np.pi), amplitudes, label=f"ξ = {xi}")
plt.axvline(x=omega_0 / (2 * np.pi), color='k', linestyle='--', label="Fréquence propre")
plt.title("Résonance : effet du taux d'amortissement xi sur l'amplitude")
plt.xlabel("Fréquence d'excitation (Hz)")
plt.ylabel("Amplitude")
plt.legend()
plt.show()
Décomposition impulsionnelle - 1ère implémentation avec integral (MATLAB)
% === Paramètres du système ===
m = 1; % masse (kg)
k = 6; % raideur (N/m)
c = 0.01; % amortissement (N·s/m)
xi = c / (2 * sqrt(k * m)); % coefficient d’amortissement
omega_n = sqrt(k / m); % pulsation propre non amortie
omega_d = omega_n * sqrt(1 - xi^2); % pulsation amortie
% === Temps et excitation ===
t_max = 20;
dt = 0.01;
t = 0:dt:t_max;
f_t = 1.5 * sin(2 * pi * t);
h_t = (1 / (m * omega_d)) * exp(-xi * omega_n * t) .* sin(omega_d * t);
response_imp = zeros(size(t));
for i = 2:length(t)
response_imp(i) = trapz(t(1:i), f_t(1:i) .* h_t(i:-1:1));
end
% === Affichage ===
figure;
plot(t, response_imp, 'r');
xlabel('Temps (s)');
ylabel('Réponse x(t)');
title('Réponse par Décomposition Impulsionnelle');
grid on;
Décomposition impulsionnelle - 2ème implémentation avec conv (MATLAB)
% Paramètres du système
m = 1;
k = 100;
c = 2;
omega0 = sqrt(k/m);
zeta = c / (2*sqrt(k*m)); % facteur d'amortissement
omega_d = omega0 * sqrt(1 - zeta^2); % pulsation amortie
% Discrétisation temporelle
dt = 0.01; % pas de temps
T_total = 10; % durée totale (s)
t = 0:dt:T_total;
% Force d'excitation (ex : sinusoïdale ou signal quelconque)
f = sin(2*pi*1.5*t);
h = (1/(m*omega_d)) * exp(-zeta*omega0*t) .* sin(omega_d*t);
x = dt * conv(f, h); % convolution et pondération par dt
x = x(1:length(t)); % tronquage pour garder même taille que f
figure;
plot(t, x, 'b', 'LineWidth', 1.5);
xlabel('Temps (s)');
ylabel('Réponse x(t)');
title('Réponse du système par décomposition impulsionnelle (convolution)');
grid on;
Décomposition indicielle (MATLAB)
m = 1;
k = 6;
c = 0.01;
xi = c / (2 * sqrt(k * m)); % coefficient d’amortissement
omega_n = sqrt(k / m);
omega_d = omega_n * sqrt(1 - xi^2);
t_max = 20;
dt = 0.01;
t = 0:dt:t_max;
f_t = 1.5 * sin(2 * pi * t);
g_t = (1 / k) * (1 - exp(-xi * omega_n * t) .* ...
(cos(omega_d * t) + (xi * omega_n / omega_d) * sin(omega_d * t)));
df_dt = [0, diff(f_t) / dt]; % approximation numérique de df/dt
response = zeros(size(t));
for i = 2:length(t)
response(i) = trapz(t(1:i), df_dt(1:i) .* g_t(i:-1:1));
end
% === Affichage de la réponse
figure;
plot(t, response, 'b', 'LineWidth', 1.5);
xlabel('Temps (s)');
ylabel('Réponse du système');
title('Réponse par Décomposition Indicielle (convolution avec df/dt)');
grid on;
Méthode d'Euler (MATLAB)
m = 1;
k = 100;
c = 2;
dt = 0.001; % pas de temps (s)
T = 5; % durée totale (s)
t = 0:dt:T;
N = length(t);
F0 = 10;
omega = 5 * 2*pi;
f = F0 * sin(omega * t);
% Initialisation des vecteurs de solution
x = zeros(1, N); % déplacement
v = zeros(1, N); % vitesse
% Conditions initiales
x(1) = 0;
v(1) = 0;
for n = 1:N-1
a = (f(n) - c*v(n) - k*x(n)) / m;
v(n+1) = v(n) + dt * a;
x(n+1) = x(n) + dt * v(n);
end
figure;
plot(t, x, 'b', 'LineWidth', 1.5);
xlabel('Temps (s)');
ylabel('Déplacement x(t) (m)');
title('Réponse du système 1DDL - Méthode d''Euler');
grid on;
Utilisation du solveur ode45 de MATLAB (basé sur Runge-Kutta 4)
m = 1;
k = 100;
c = 2;
F0 = 10;
omega = 5 * 2*pi;
f = @(t) F0 * sin(omega * t);
Tmax = 5;
tspan = [0 Tmax];
% Cond intiales
x0 = [0; 0];
odefun = @(t, x) [ ...
x(2); % dx/dt = v
(1/m) * (f(t) - c*x(2) - k*x(1)) % dv/dt
];
% Résolution avec ode45
[t, sol] = ode45(odefun, tspan, x0);
figure;
plot(t, sol(:,1), 'b', 'LineWidth', 1.5);
xlabel('Temps (s)');
ylabel('Déplacement x(t) (m)');
title('Réponse du système 1DDL - Méthode ode45');
grid on;
Gain de \(H_2(z)\) pour différentes valeurs de \(\eta_1\) (MATLAB)
eta1_values = [0.1, 0.3, 0.6]; % Différentes valeurs de eta_1
beta = 0.953;
alpha = 0.1;
for eta1 = eta1_values
H1 = (z.^2) ./ (-z.^2 + 2*1i*eta1*beta.*z + beta^2);
H2 = (z.^2) ./ ((1 + alpha + alpha.*H1).*z.^2 - 1);
gain = 20 * log10(abs(H2));
semilogx(z, gain, 'DisplayName', sprintf('\\eta_1 = %.1f', eta1));
end
xlabel('z = \omega / \omega_0');
ylabel('Gain (dB)');
title('Gain de H_2(z) pour différentes valeurs de \eta_1');
grid on;
legend('show');
Bibliographie
- Clough, R. W., & Penzien, J. (1993). Dynamics of Structures. McGraw-Hill.
- Chopra, A. K. (2017). Dynamics of Structures: Theory and Applications to Earthquake Engineering. Prentice Hall.
- Tout le cours de Physique (MPSI-PCSI), Lionel Jannaud, Chapitre 17 (Régime sinusoïdal forcé), Editions Ellipses
- La mécanique et les ondes élastiques en prépa et à l'agrégation, Thierry Meyer, (Chapitre 10 - Systèmes à 1DDL), Editions Ellipses
- Dynamique des Solides et des Structures, Sylvain Drapier, https://www.emse.fr/drapier/indexfichiers/CoursPDF/Dynamique-3A/Dynamique-SDrapier-janvier2012.pdf, (Chapitre 2, Partie II - Systèmes à NDDL)
- Sujet de Physique du Concours Mines-Ponts 2007 (Filière MP) - Sujet : http://www.klubprepa.fr/Site/Document/ChargementExtrait.aspx?IdDocument=6983
- Des tours qui chavirent, Jean-Michel Courty et Édouard Kierlik, POUR LA SCIENCE N° 356, https://www.pourlascience.fr/sd/physique/des-tours-qui-chavirent-2964.php
