Il y a quelques années, lorsque je préparais les concours, j’avais travaillé sur le sujet de physique MP du concours X-ENS 2018 consacré à la tuyère du moteur Vulcain d’Ariane 5 (le sujet original est disponible ici). Je m’en souviens bien : le thème de la propulsion m’avait déjà beaucoup plu, et ce sujet m’avait donné pour la première fois une vision claire de la manière dont un écoulement peut être accéléré jusqu’au régime supersonique simplement grâce à une géométrie adaptée.
Aujourd’hui, en Master, et avec un peu plus de recul et surtout avec de nouvelles connaissances en mécanique des fluides numérique et en CFD, j’ai eu envie de revisiter ce sujet. Je reprends donc ici la progression du problème, en m’appuyant notamment sur les relations dérivées dans les questions Q5 à Q11 et sur l’étude de l’adaptation en pression des questions Q12 à Q17, mais en les prolongeant cette fois par une modélisation numérique sous Mathematica.
Équations fondamentales de l’écoulement isentropique dans une tuyère de Laval
On modélise l’écoulement dans la tuyère comme un écoulement de gaz parfait, unidimensionnel, stationnaire, adiabatique et réversible. L’entropie est donc constante le long de la ligne de courant : on parle d’écoulement isentropique. La section de la tuyère, notée \(A(x)\), varie avec l’abscisse \(x\), mesurée à partir de la sortie de la chambre de combustion.
La première relation clé est la conservation du débit massique. À toute abscisse \(x\), on a
\(\dot m = \rho(x)\, v(x)\, A(x).\)
Dans un régime stationnaire, \(\dot m\) est constant le long de la tuyère. Cela signifie que toute variation de section doit être compensée par une variation de densité ou de vitesse. C’est cette contrainte qui, combinée au caractère compressible du gaz, permet d’accélérer l’écoulement jusqu’au régime supersonique.
La seconde relation fondamentale vient de la conservation de l’énergie sous forme d’enthalpie de stagnation. Pour un gaz parfait, l’enthalpie massique s’écrit \(h = C_p T\), et l’énergie totale (enthalpie + énergie cinétique) se conserve le long de la tuyère :
\(h_0 = h + \dfrac{v^2}{2} = C_p T_0 = C_p T + \dfrac{v^2}{2}.\)
On introduit alors la célérité du son \(c = \sqrt{\gamma R T}\) et le nombre de Mach \(M = v/c\). En remplaçant \(v = Mc\) dans l’équation précédente, on obtient, après simplification,
\(1 + \dfrac{\gamma - 1}{2} M^2 = \dfrac{T_0}{T}.\)
Cette relation exprime le lien entre la température locale du gaz et sa vitesse. Plus le nombre de Mach augmente, plus la température chute et plus une partie de l’énergie interne est convertie en énergie cinétique.
En combinant cette expression avec la loi des gaz parfaits et la condition isentropique \(P/\rho^\gamma = \text{cste}\), on obtient les relations isentropiques classiques :
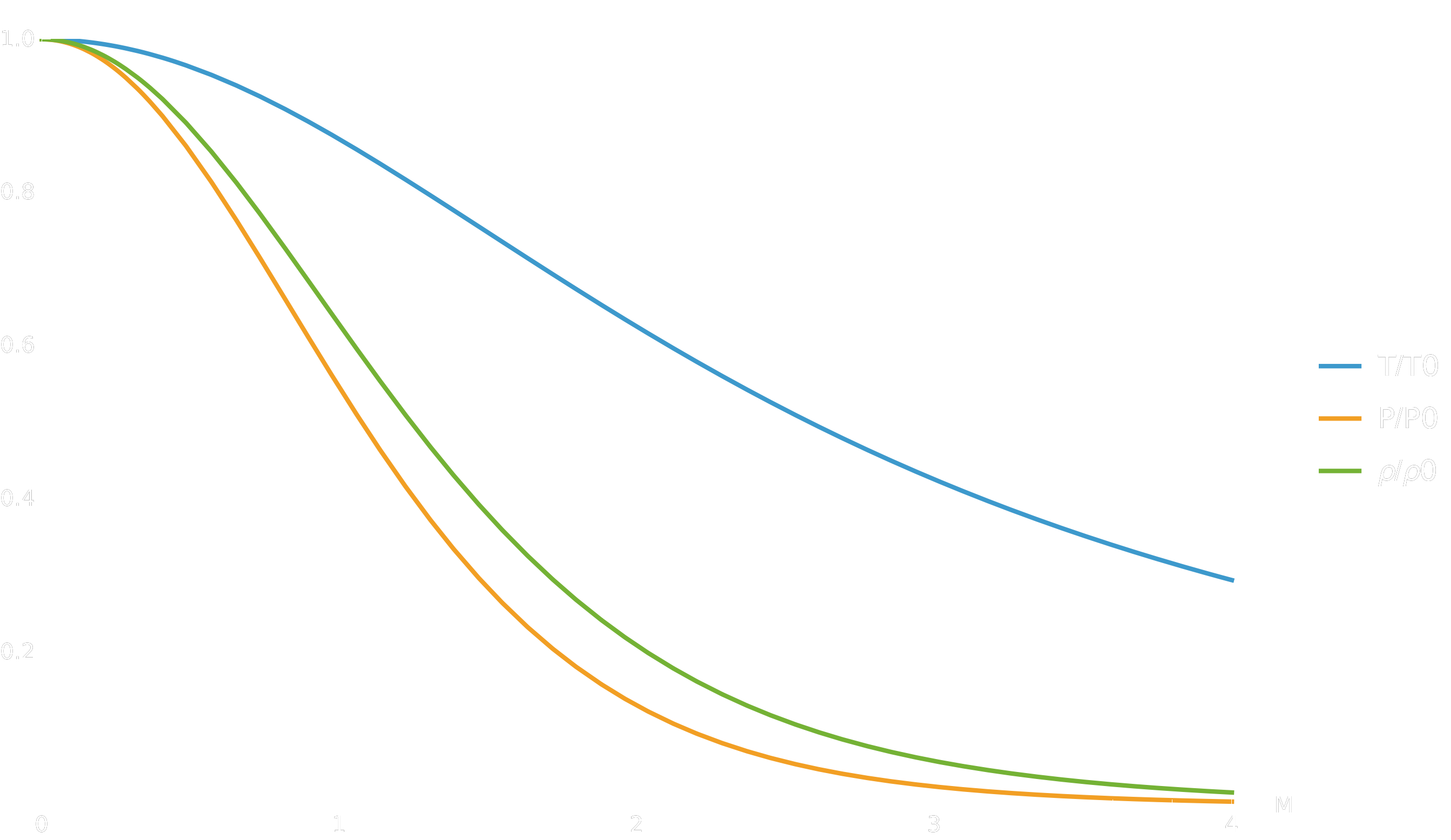
\(\dfrac{T}{T_0} = \dfrac{1}{1 + \dfrac{\gamma-1}{2}M^2},\)
\(\dfrac{P}{P_0} = \left(\dfrac{T}{T_0}\right)^{\frac{\gamma}{\gamma-1}},\quad \dfrac{\rho}{\rho_0} = \left(\dfrac{T}{T_0}\right)^{\frac{1}{\gamma-1}}.\)
Ces expressions seront au cœur de l’implémentation numérique : elles permettent de déduire pression, température et densité à partir du nombre de Mach, pour des conditions de stagnation données \((P_0, T_0)\).
gamma = 1.3;
alpha = (gamma - 1)/2;
tOverT0[M_] := 1/(1 + alpha*M^2);
pOverP0[M_] := tOverT0[M]^(gamma/(gamma - 1));
rhoOverRho0[M_] := tOverT0[M]^(1/(gamma - 1));
Plot[{tOverT0[M], pOverP0[M], rhoOverRho0[M]}, {M, 0, 4},
PlotLegends -> {"T/T0", "P/P0", "ρ/ρ0"},
AxesLabel -> {"M", ""},
PlotRange -> {0, 1},
ImageSize -> Large]
Condition critique au col
On s’intéresse maintenant à la question suivante : pour une pression de stagnation donnée, existe-t-il un débit maximal que la tuyère peut laisser passer ? Autrement dit, peut-on “saturer” le débit massique en jouant uniquement sur la pression de chambre ? La réponse est oui, et ce phénomène est lié à l’apparition du régime sonique au col.
En repartant de la conservation du débit massique et des relations isentropiques, on peut écrire le débit sous la forme
\(\dot m = A P_0 \sqrt{\dfrac{\gamma}{R T_0}}\, M \left( 1 + \dfrac{\gamma - 1}{2}M^2 \right)^{-\frac{\gamma+1}{2(\gamma-1)}}.\)
Pour un conduit donné, \(A\) est fixée. Le débit massique dépend donc uniquement du nombre de Mach \(M\) et des conditions de stagnation. Pour trouver le débit maximal, on dérive \(\dot m(M)\) par rapport à \(M\) et on impose que la dérivée s’annule. Le calcul, bien que un peu technique, montre que l’extremum est atteint pour
\(M = 1.\)
On note la section correspondante \(A^\ast\). Physiquement, cela signifie qu’au niveau de cette section minimale (le col de la tuyère), l’écoulement devient sonique. Au-delà, même si l’on augmente la pression de stagnation dans la chambre, le débit massique ne peut plus augmenter : l’écoulement est « étranglé » (choked flow). L’énergie supplémentaire se traduit alors par une augmentation du Mach et de la vitesse dans la partie divergente, et donc par une plus grande vitesse d’éjection.
gamma = 1.3;
alpha = (gamma - 1)/2;
massFlowNonDim[M_] :=
M*(1 + alpha*M^2)^(- (gamma + 1)/(2*(gamma - 1)));
Plot[massFlowNonDim[M], {M, 0.01, 4},
AxesLabel -> {"M", "ṁ / (A P0 Sqrt[γ/(R T0)])"},
PlotRange -> All,
Epilog -> {Red, PointSize[Medium], Point[{1, massFlowNonDim[1]}]},
ImageSize -> Large]
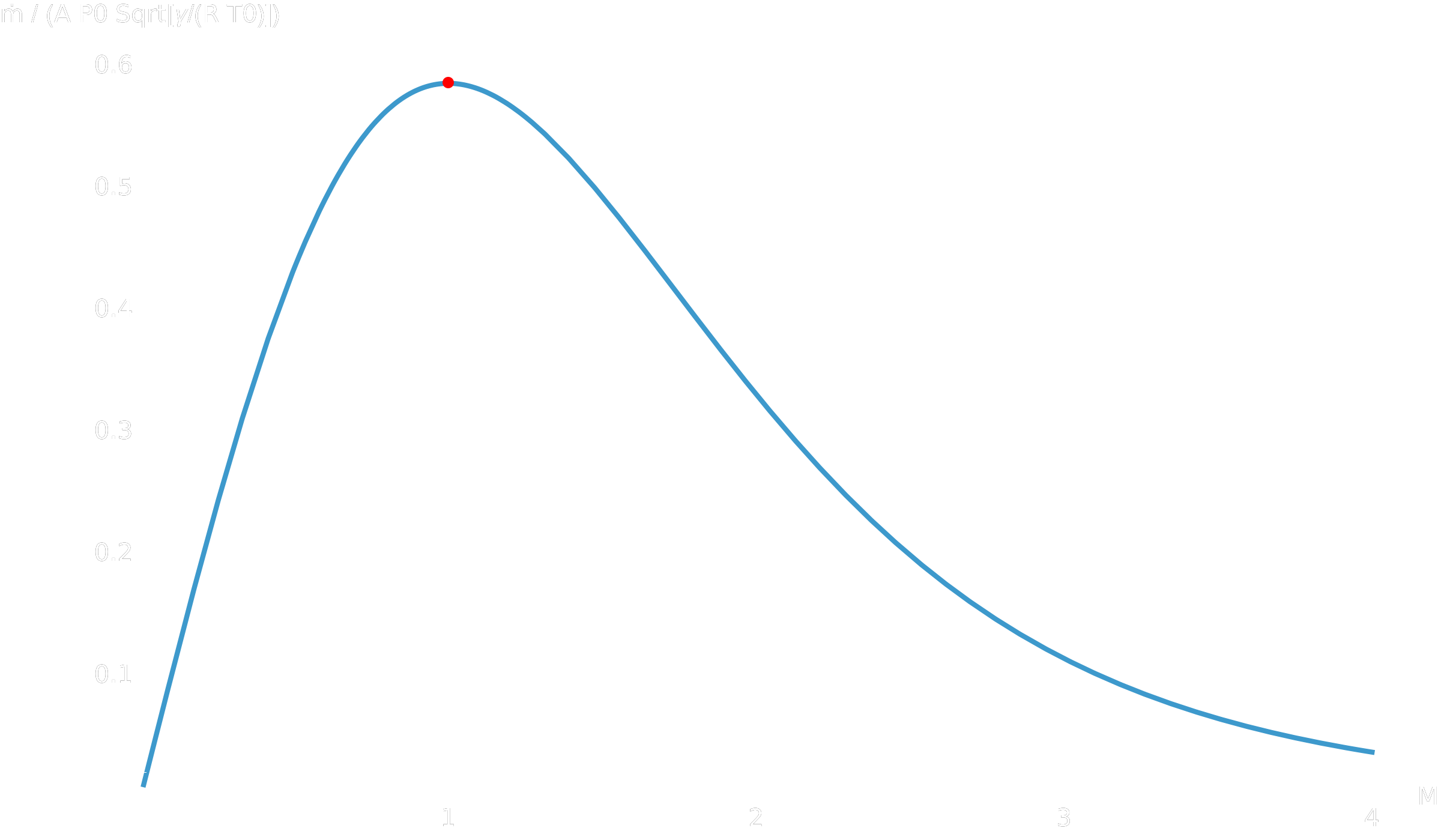
La figure générée par ce code montre clairement un maximum de débit réduit pour \(M = 1\). C’est ce comportement qui justifie le choix d’une tuyère convergente-divergente en propulsion spatiale : le col impose le régime sonique, la partie divergente développe ensuite le régime supersonique.
Relation d’aire : l’équation géométrique fondamentale A(M)
Pour relier la géométrie de la tuyère à l’état de l’écoulement, on part de la conservation du débit massique \(\dot m = \rho v A\). En prenant une différentielle logarithmique, on obtient
\(\dfrac{d\rho}{\rho} + \dfrac{dv}{v} + \dfrac{dA}{A} = 0.\)
La relation de Hugoniot, issue du principe fondamental de la dynamique appliqué à un fluide en écoulement unidimensionnel, fournit un lien entre variations de vitesse et de pression :
\(\rho v\, dv = -\, dP.\)
En utilisant la loi isentropique \(dP = c^2\, d\rho\) avec \(c^2 = \gamma P/\rho\), on peut éliminer \(dP\) et \(d\rho\) au profit de \(dv\) et \(M\). Après quelques manipulations algébriques, on obtient la forme classique de la relation de Hugoniot :
\(\dfrac{dA}{A} = \left(M^2 - 1\right)\, \dfrac{dv}{v}.\)
Cette équation montre que, pour un écoulement subsonique (\(M < 1\)), une diminution de section (\(dA < 0\)) impose une augmentation de vitesse (\(dv > 0\)). Dans le régime supersonique (\(M > 1\)), c’est l’inverse : l’augmentation de vitesse est associée à une augmentation de section. C’est ce qui rend possible l’accélération supersonique dans une tuyère divergente.
Pour se débarrasser de \(v\), on combine la relation ci-dessus avec les relations isentropiques et la définition du Mach. On peut montrer que
\(\dfrac{dA}{A} = \dfrac{M^2 - 1}{M\,(1 + \alpha M^2)}\, \dfrac{dM}{M}, \quad \alpha = \dfrac{\gamma - 1}{2}.\)
Il s’agit d’une équation différentielle à variables séparées. En intégrant entre un état sonique (\(M = 1\), \(A = A^\ast\)) et un état générique, on obtient l’expression fermée du rapport de sections \(\dfrac{A}{A^\ast}\) en fonction de \(M\). Pour un gaz parfait classique, cette relation peut s’écrire sous la forme
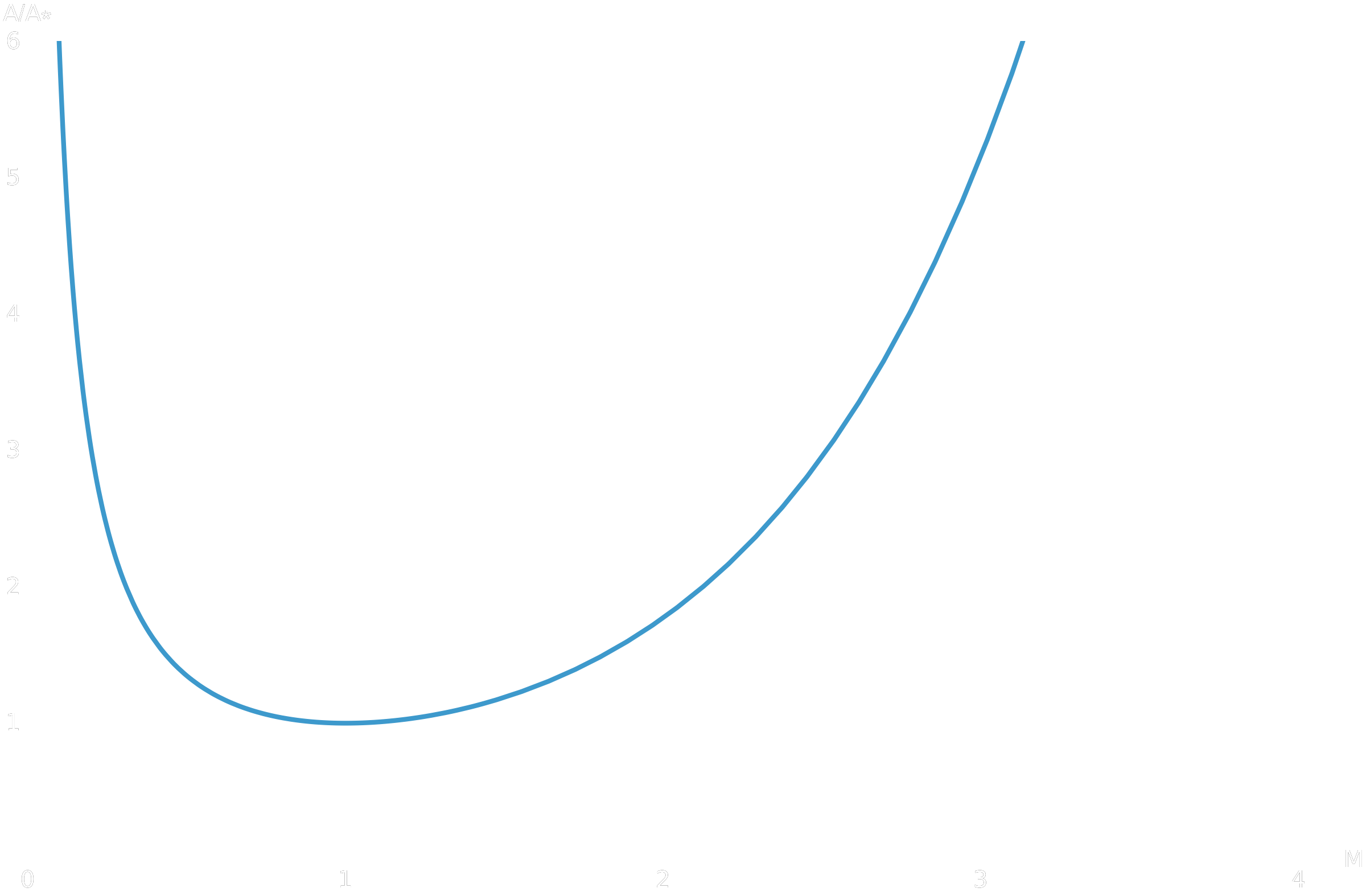
\(\dfrac{A}{A^\ast}(M) = \dfrac{1}{M} \left(\dfrac{2}{\gamma+1}\, \left[1 + \dfrac{\gamma-1}{2}M^2\right]\right)^{\frac{\gamma+1}{2(\gamma-1)}}.\)
Cette formule est le cœur de la modélisation géométrique de la tuyère : à partir d’un Mach, on peut calculer la section relative nécessaire, et inversement, pour une géométrie donnée, on peut retrouver le profil de Mach par inversion numérique.
gamma = 1.3;
alpha = (gamma - 1)/2;
AoverAstar[M_] :=
(1/M) * (2/(gamma + 1) * (1 + alpha*M^2))^((gamma + 1)/(2*(gamma - 1)));
Plot[AoverAstar[M], {M, 0.01, 4},
AxesLabel -> {"M", "A/A*"},
PlotRange -> {0, 6},
ImageSize -> Large]
Pression de sortie et adaptation à l’environnement
La pression à la sortie de la tuyère est entièrement déterminée par le Mach de sortie \(M_s\) et par la pression de stagnation \(P_0\) dans la chambre. La relation isentropique donne
\(P_s = P_0 \left(1 + \dfrac{\gamma-1}{2}M_s^2\right)^{-\frac{\gamma}{\gamma-1}}.\)
Pour analyser le fonctionnement réel, il faut comparer cette pression de sortie à la pression extérieure \(P_e\) (par exemple \(1\) bar au niveau de la mer). On distingue alors trois régimes classiques :
Si \(P_s = P_e\), la tuyère est dite adaptée : le jet s’épanouit sans onde de choc ni zone de détente majeure. Si \(P_s > P_e\), la sortie est sous-détendue : les gaz continuent de se détendre après la lèvre de tuyère, générant un motif d’ondes d’expansion et éventuellement de chocs obliques. Si enfin \(P_s < P_e\), la tuyère est sur-détendue : un choc normal peut apparaître dans la partie divergente, avec des pertes importantes.
Le moteur Vulcain est conçu pour être adapté à haute altitude, au prix d’un fonctionnement fortement sous-détendu au niveau du sol : la pression de sortie y est très supérieure à la pression atmosphérique. Cela maximise les performances en fin de trajectoire, là où la poussée du moteur principal joue un rôle déterminant, tout en étant compensé au décollage par la poussée des boosters à poudre.
gamma = 1.3;
alpha = (gamma - 1)/2;
Ps[Ms_, P0_] := P0*(1 + alpha*Ms^2)^(-gamma/(gamma - 1));
P0 = 1.1*10^7; (* Pa, valeur typique issue du sujet X-ENS *)
Plot[Ps[Ms, P0]/10^5, {Ms, 0, 5},
AxesLabel -> {"M_s", "P_s (bar)"},
PlotRange -> {0, 200},
ImageSize -> Large,
Epilog -> {
Dashed, Gray, Line[{{0, 1}, {5, 1}}] (* Pe = 1 bar *)
}]
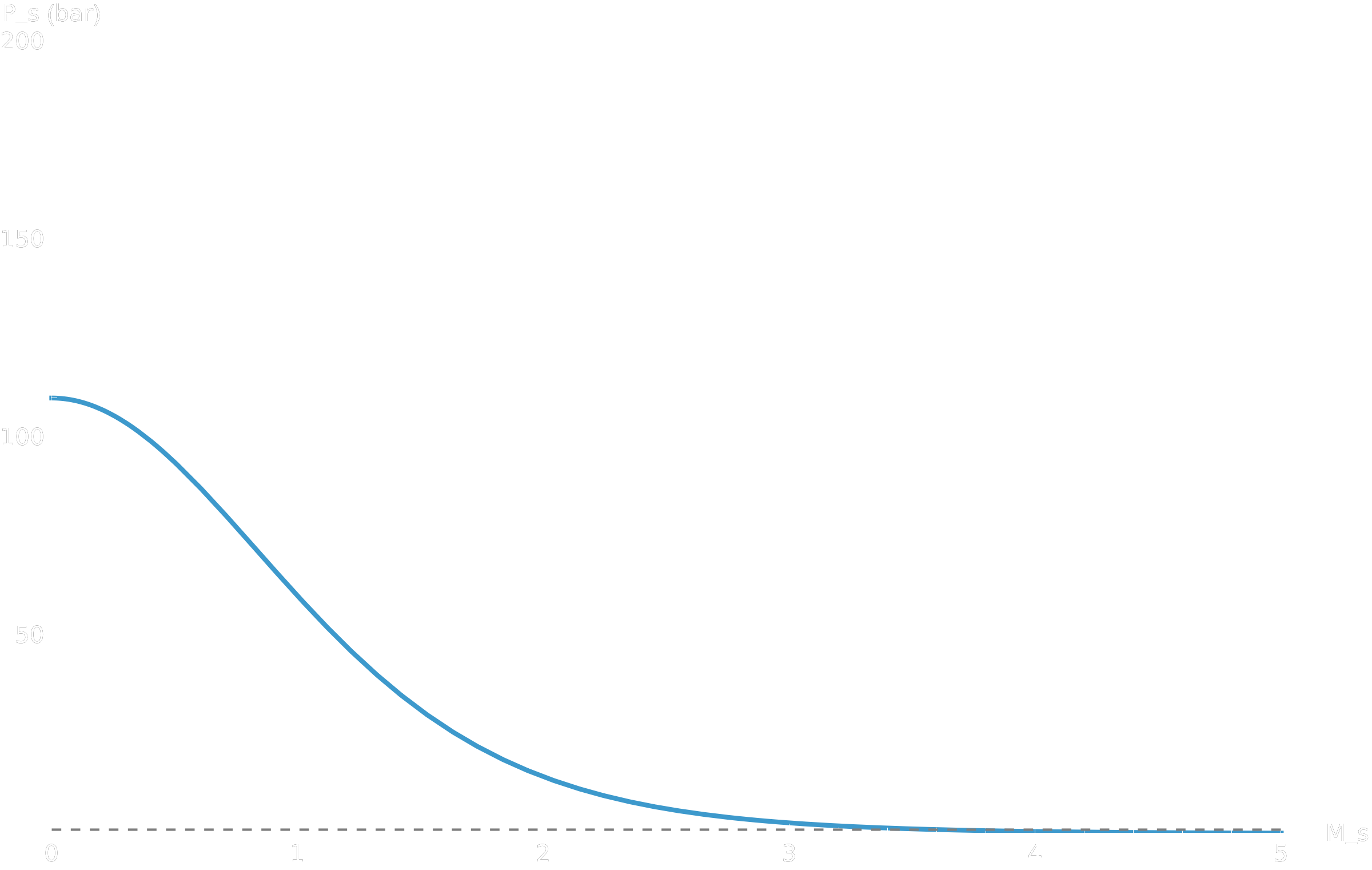
Le tracé de \(P_s\) en fonction de \(M_s\) permet de visualiser, pour une pression de chambre donnée, les valeurs de Mach de sortie pour lesquelles la tuyère est adaptée (intersection avec la droite \(P_s = P_e\)) ou sous/sur-détendue.
Poussée de la tuyère : terme cinétique et terme de pression
La poussée totale fournie par la tuyère s’écrit, en négligeant le poids du gaz dans la tuyère,
\(F = \dot{m}\, v_s + (P_s - P_e)\, A_s.\)
Le premier terme, \(\dot m\, v_s\), traduit la contribution de la quantité de mouvement des gaz éjectés : c’est la conversion de l’énergie interne en énergie cinétique. Le second terme, \((P_s - P_e)\,A_s\), représente la force résultante due à la différence de pression entre les gaz de sortie et l’atmosphère sur la surface de la section de sortie.
En utilisant les relations isentropiques, on peut exprimer \(v_s\) et \(P_s\) en fonction de \(M_s\). La vitesse de sortie vaut par exemple
\(v_s = M_s\, c_s = M_s \sqrt{\gamma R T_s} = M_s \sqrt{\gamma R T_0\, \dfrac{1}{1 + \frac{\gamma-1}{2}M_s^2}}.\)
En pratique, il est souvent plus simple de manipuler numériquement ces formules plutôt que de chercher une expression symbolique explicite pour \(F\) en fonction de \(A_s/A^\ast\). C’est précisément ce que permet Mathematica : pour un jeu de paramètres donné \((P_0, T_0, \gamma, \dot m, A^\ast)\), on peut balayer différentes sections de sortie \(A_s\), calculer le Mach associé via la relation d’aire, puis en déduire \(v_s\), \(P_s\) et la poussée.
gamma = 1.3;
alpha = (gamma - 1)/2;
R = 462.; (* vapeur d'eau, comme dans le sujet X-ENS *)
P0 = 1.1*10^7; (* Pa *)
T0 = 3500.; (* K *)
mdot = 250.; (* kg/s, débit du sujet *)
AoverAstar[M_] :=
(1/M) * (2/(gamma + 1) * (1 + alpha*M^2))^((gamma + 1)/(2*(gamma - 1)));
(* inversion numérique : trouver M correspondant à A_s/A* donné *)
machFromAreaRatio[k_] :=
FindRoot[AoverAstar[M] == k, {M, 3}][[1, 2]]; (* branche supersonique *)
Ps[Ms_] := P0*(1 + alpha*Ms^2)^(-gamma/(gamma - 1));
vs[Ms_] := Ms*Sqrt[gamma*R*T0/(1 + alpha*Ms^2)];
thrust[k_, Pe_] := Module[{Ms, As, PsVal, vsVal},
Ms = machFromAreaRatio[k];
As = k; (* A_s/A*; pour une analyse non dimensionnée on peut prendre A* = 1 *)
PsVal = Ps[Ms];
vsVal = vs[Ms];
mdot*vsVal + (PsVal - Pe)*As
];
Pe = 10^5; (* Pa, pression extérieure ~ 1 bar *)
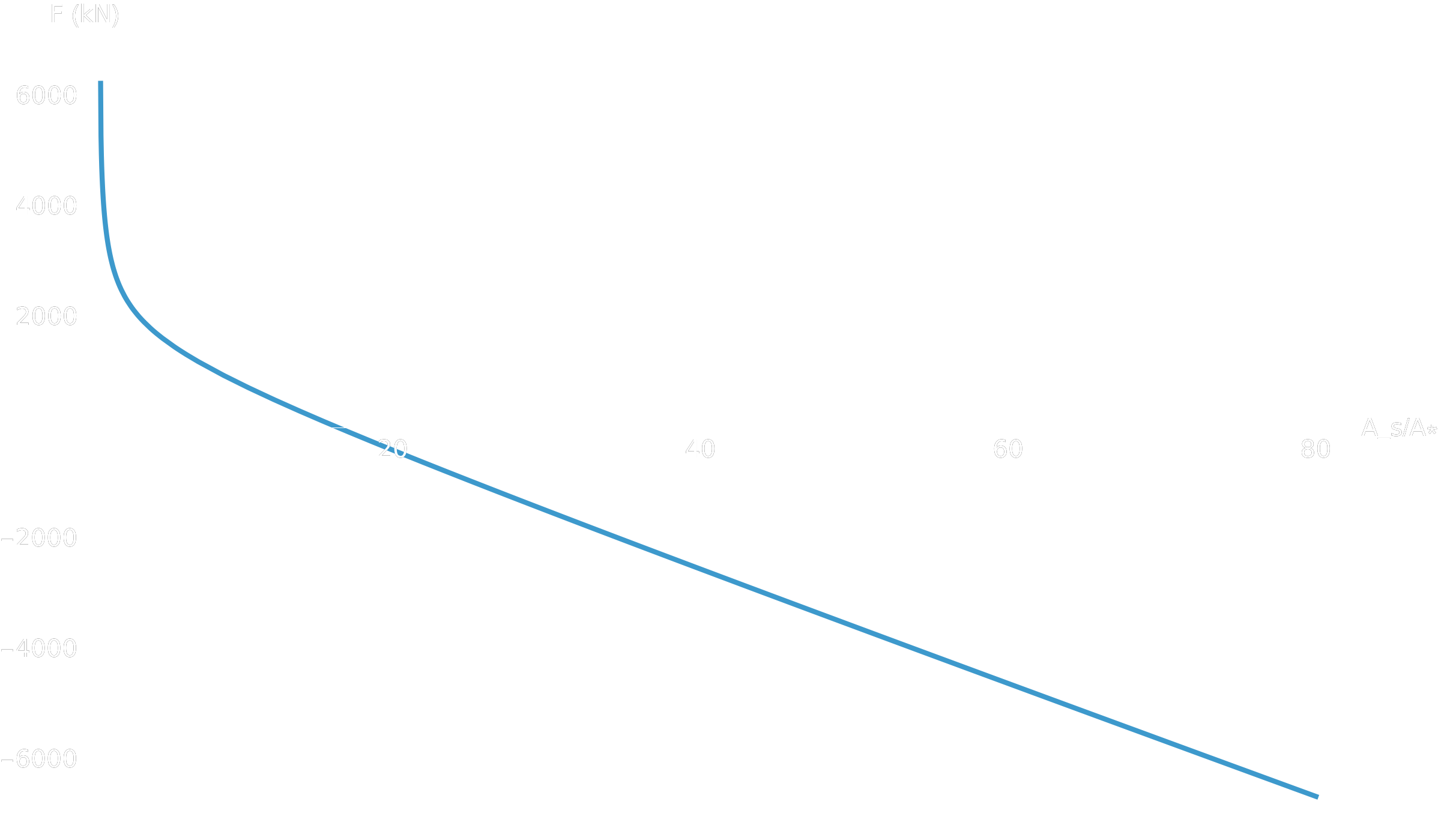
Plot[thrust[k, Pe]/10^3, {k, 1, 80},
AxesLabel -> {"A_s/A*", "F (kN)"},
PlotRange -> All,
ImageSize -> Large]